Когда корабль тонет или пропадает в море, поисково-спасательные группы часто полагаются на компьютерные модели, чтобы определить, где искать выживших. Используемые в настоящее время модели включают данные со спутников и морских датчиков для прогнозирования траектории дрейфующего объекта, создавая карты областей, где он наиболее вероятно может быть обнаружен. Если первоначальный поиск оказался неудачным, модели включают эту информацию, чтобы обновить свои прогнозы.
Математические значения знаков дроби критского линейного письма А.
Недавнее исследование группы ученых из Болонского университета, пролило новый свет на минойскую систему дробей, одну из выдающихся загадок, связанных с древним написанием чисел.
Математик представит доказательство гипотезы Sensitivity Conjecture.
Гипотеза о чувствительности The Sensitivity Conjecture является одной из самых важных и сбивающих с толку открытых проблем теоретической информатики на протяжении почти трех десятилетий. Похоже, что она наконец встретит свое решение благодаря работе Хао Хуанга, доцента математики в Университете Эмори.
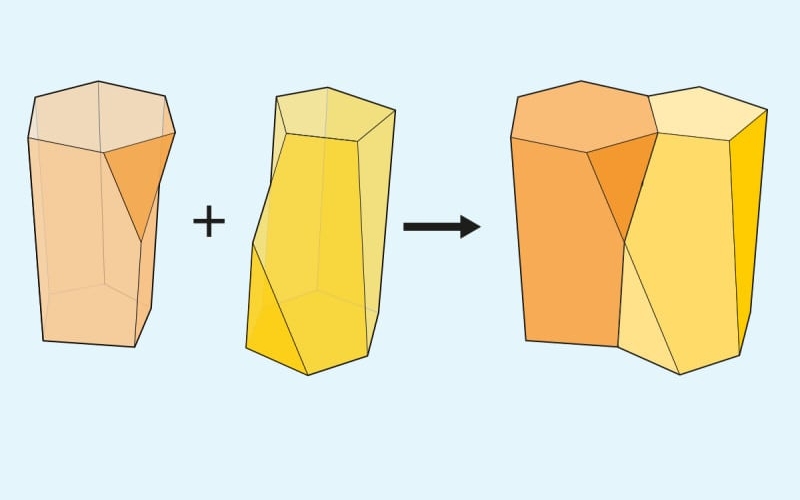
Ученые раскрыли необычные свойства недавно идентифицированной трехмерной формы, называемой «scutoid».
Исследователи обнаружили новую геометрическую форму, которая скрывалась у всех на виду. Открытие этой фигуры может иметь многочисленные применения в разных научных областях и может быть полезным в попытке выращивать искусственные био ткани и органы в лаборатории.
Использование математических формул для прогнозирования землетрясений.
Команда исследователей в Центре Лайелла в Эдинбурге разработала способ использования математических формул для прогнозирования вероятности землетрясения. В новом исследовании группа ученых описывает перевод движения определенного типа породы в математические уравнения, что привело к созданию прогнозирующей формулы.
Математики описали процесс и вывели формулу, по которой лопаются пузыри.
Понимание динамики разрыва пузырьков может дать критическое понимание некоторых процессов в целом ряде областей науки от океанографии до науки об атмосфере, но механизмы, которые приводят к окончательному схлопыванию, сложны и трудны для описания.
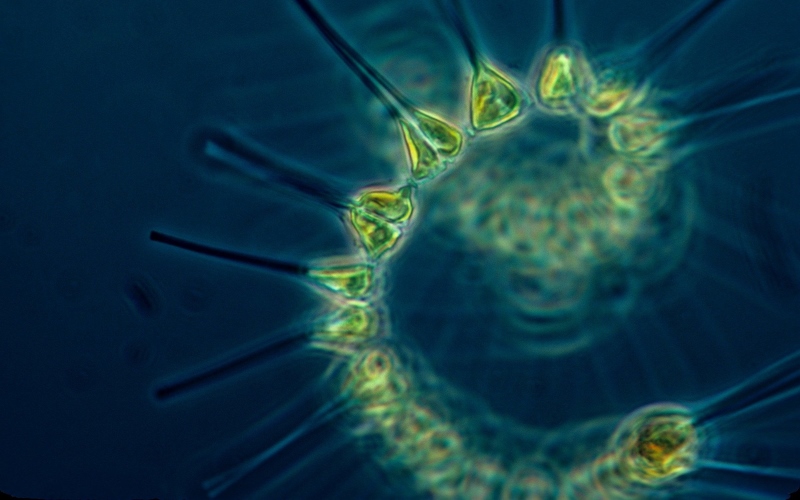
Математики создали концептуальную модель, объясняющую парадокс планктона.
Пара исследователей, один из Центра Саймонса для изучения живых машин в Индии, другой из Университета штата Иллинойс в США, построила модель, объясняющую парадокс планктона. В своей статье, опубликованной в журнале Physical Review Letters, Акшит Гоял и Сергей Маслов описывают свою модель и насколько хорошо, она изображает фактические сообщества бактерий, по их мнению.