Если вам сложно оптимально использовать пространство при вырезании большого количества фигур или упаковке ящика, не стесняйтесь сдаваться.
Три европейских исследователя предполагают, что это может быть слишком сложно, если только не случайность, особенно если формы имеют необычную форму.
По словам Миккеля Абрахамсена из Датского университета Копенгагена, задачи упаковки - это класс задач оптимизации, и математики решали их на протяжении веков.
«Хотя алгоритмы позволяют нам решать серьезные сложные проблемы, это одна из тех проблем, которые для современных компьютеров остаются невыносимыми. На данный момент невозможно оптимально упаковать более пяти-десяти объектов, и наш результат предполагает, что это число, вероятно, пока не сильно увеличится».
Абрахамсен - ведущий автор статьи, представленной на симпозиуме IEEE по основам информатики и доступной на сервере предварительной печати arXiv. Его соавторами являются Тилльман Мильцов из Утрехтского университета в Нидерландах и Надя Зайферт из Свободного университета Германии.
Говоря математически они пишут, что «многие задачи естественной двумерной упаковки алгоритмически эквивалентны поиску действительных корней многомерных многочленов».
Это, конечно, серьезная проблема в отраслях, которым необходимо вырезать материалы или упаковывать продукты с минимальным количеством отходов.
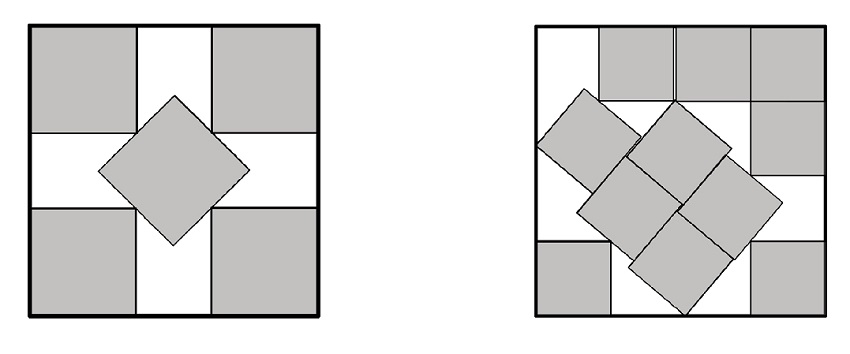
Оптимальная упаковка пяти квадратов и самая известная в настоящее время упаковка из 11 квадратов в большой квадрат. Фото: Mikkel Abrahamsen
«Мы знаем размер самого маленького квадратного контейнера, в который мы можем упаковать до 10 квадратных поддонов», - говорит Абрахамсен, но, просто добавив еще один поддон, невозможно рассчитать оптимальный размер контейнера.
«По мере добавления поддонов время расчета увеличивается экспоненциально. Даже лучшие компьютеры не могут угнаться за ними. Теоретически это возможно. Но, судя по скорости роста вычислительной мощности, вероятно, пройдут миллионы лет, прежде чем мы сможем оптимизировать обработку нескольких дополнительных объектов».
Он предполагает, что работа со сложными формами усугубляет проблему. Оптимальные решения сегодня можно найти не более чем для четырех объектов.
Причина? «Наше исследование доказывает, что проблема имеет характер, который мы в математике называем непрерывным, что, в двух словах, означает, что нужно знать все координаты, в которые могут быть помещены [объекты], и все углы, под которыми их можно вращать».
По словам исследователей, поскольку возможных комбинаций бесконечно, нет никакого способа составить список всех мест, которые необходимо попробовать, чтобы найти оптимальное решение. Вместо этого алгоритмы, которые решают проблемы упаковки оптимальным образом, должны быть более аналитическими, что отнимает много времени.
Это контрастирует со многими другими алгоритмическими проблемами, где можно попробовать ограниченное количество комбинаций, прежде чем найти оптимальную.
Так что на практике нет решений лучше, чем те, которые могут придумать люди.
«Как в промышленности, так и на кухне, мы должны продолжать довольствоваться нашими неоптимальными решениями и быть уверены, что мы, люди, все еще лучше, чем компьютеры для таких задач - пока что», - заключает Абрахамсен.
Источник: Cosmos Magazine













