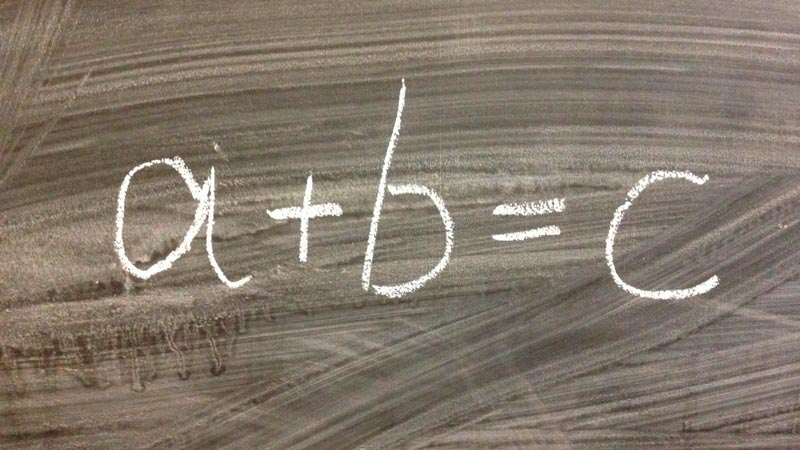Синъити Мотидзуки из Киотского университета в Японии, которого сравнивают с российским ученым Григорием Перельманом, в беседе по Skype объяснил своим коллегам предложенное три года назад решение гипотезы Эстерле-Массера (abc-гипотезы), сформулированной 27 лет назад . Большинство коллег не поняли доказательство математика, сообщает Nature News.
Коллеги математика по-разному оценили объяснения Мотидзуки. Большинство из них его не поняли и разочаровались, а некоторые и вовсе сочли его выступления фарсом. Главные недовольства математиков свелись к чрезмерно абстрактному языку доказательства abc-гипотезы и формальному стилю коммуникации Мотидзуки со своими коллегами.
Семинар, прошедший 7-11 декабря 2015 года по Skype, был организован в Оксфорде Математическим институтом Клэя. На нем математики задавали Мотидзуки интересующие их вопросы о гипотезе Эстерле-Массера и слушали объяснения ученого. Сам автор возможного доказательства при этом находился в Японии. Ученые планируют продолжить изучение работ Мотидзуки.
Доказательство Мотидзуки занимает более 500 страниц текста, а понять и проверить его способно небольшое число математиков. У эксперта может уйти до 500 часов работы для понимания доказательства, тогда как у математика-аспиранта это займет около десяти лет. В настоящее время только четыре математика сообщили, что прочитали и поняли доказательство abc-гипотезы Мотидзуки. Принятию работы ученого научным сообществом мешает то, что математик отказывается покидать территорию страны, не встречается с прессой и нерегулярно отвечает на сообщения электронной почты.
Независимо друг от друга abc-гипотеза предложена математиками Дэвидом Массером в 1985 году и Джозефом Эстерле в 1988 году, а ее решение составляет одну из главных проблем теории чисел. Гипотеза утверждает, что для любого действительного числа r > 1 существует не более конечного числа троек натуральных чисел a, b и c таких, что для них выполняются условия: a + b = c; a, b и c взаимно просты в совокупности (то есть у них нет общих делителей) и c > rad (abc)r.
Радикалом (rad) натурального числа N называется число, которое представляет собой произведение всех различных простых (отличных от единицы чисел, делящихся только на себя и на единицу) делителей числа N. Например, rad(15) = 15, так как у этого числа простые делители 3 и 5, а rad(18) = 6, поскольку простых делителей у числа 18 ровно два — это 3 и 2.
Гипотеза Эстерле-Массера важна для теории диофантовых уравнений, а ее справедливость позволит провести еще одно доказательство великой теоремы Ферма для больших степеней.
Мотидзуки родился в Токио в 1969 году. Детство провел в США, где окончил среднюю школу в Нью-Гемпшире. В 16 лет поступил на математический факультет Принстонского университета. В 1994 году вернулся в Японию. Коллеги ученого отмечают высокую сконцентрированность Мотидзуки при решении математических задач и его неприятие американской культуры.
Источник: Lenta.ru